amplitude and dB
As seen in lesson 3, there are still a couple of measurements that we need to know in order to understand sound's behaviour, one of which is its amplitude.
The amplitude of a sound wave is strictly connected to how loud that sound is perceived. In order to introduce a unit of measure for sound loudness, we need to understand how our ears perceive sound. More will be said about the anatomy of the ear, for now let's quickly focus on the eardrum: a very thin membrane that is able to detect even the slightest air vibration. When a vibrating object generates vibrations in the air, the vibrating air hits our eardrums, whose movements are then transduced into electric impulses that are transmitted to our brain which interprets them as sound.
Our perception of sound, is connected with the pressure exercised on our eardrums, but not in direct proportion. If the relation between air pressure and perceived loudness were linear (or direct), we could say that applying twice as much pressure on our eardrum would result in a twice as loud sound. Well, it is not quite so: the pressure exercised on our eardrums and the loudness that we feel are connected by a logarithmic proportion, not by a direct one. At very low pressure levels, we are able to distinguish slight variations very clearly. The higher the pressure, the more the pressure must be increased in order for us to perceive the same increment in loudness.
Confused? Look at the following graph:
As you can see, in this graph the pressure (x) and the perceived loudness (y) are directly proportional, so when one increases, the other one increases of the same amount.
OUR EARS DON'T WORK LIKE THAT!!!!
This is more like it:
Let's not talk about units of measure for the moment (this graph is for demonstration only), but according to this graph, to a loudness of 2,5 corresponds a pressure of 1,7 (P1). In order to feel the sound twice as loud, we need the pressure to rise up to 3,14(P2): an increment of 1,44 units of pressure, which we will perceive with a loudness of 5. Now, if we would want to feel the sound with a loudness of 10, hence doubling the current loudness, the pressure exercised on our eardrums must be 10 units of pressure (P3), an increment of 6,86. Doubling this last value of loudness would make our eardrums bare a pressure value of about 100 units of pressure (not on graph): an increment of 90 units!
So, let's compare the two proportions in a chart:
This is the way our ears work, so the kind of values we have do deal with range from extremely low to extremely high, which is not exactly convenient when it comes to operations and calculations. If we could have a logarithmic scale to measure the pressure variations we could kind of 'rectify' the curve on the graph and have much practical values to deal with.
Rectified graph:
As you can see, by applying a logarithmic scale to the y axis, we are here dealing with much more convenient numbers and values, and we can also see pressure value P4, which was not visible using a linear scale.
This is why at Bell Telephone Laboratories telecommunication engineers have elaborated a unit of measure that suits the ear's behaviour. The Bel.
The Bel (in honour of Alexander Graham Bell) is a very particular measurement scale, mostly because is used to meter relative and not absolute values.
A Bel, or its submultiple decibel (dB), is not a unit of measurement itself, since it does not measure anything in particular: it expresses a logarithmic relationship between a given value and its reference value. Those values can be any kind of values: voltage, power, intensity, and, in our case, sound pressure or sound intensity. The reference value (the 0dB) is usually the minimum value employed for that measurement. In case of sound pressure, the minimum value is defined as the pressure exercised on the human eardrum by the softest sound audible. In other words, it is the softest sound a human can hear. By convention this sound pressure level is set at 20 micropascal (20 µPa).
A Pascal (Pa) is a unit of pressure:
'N' stands for Newton, a unit of force, defined as such:
"A force of one Newton will accelerate a mass of one kilogram at the rate of one meter per second per second" [2]
Another way we can measure the power of a sound wave is measuring its intensity: sound intensity is a measure of sound power per unit area and it is measured in Watts per square meter.
1W = 1Joule/1s
"A joule is the amount of energy necessary to exert a force of 1 Newton for a distance of 1 meter" [3] so:
1W = 1N*1m/1s
Intensity is the amount of energy that passes through a square meter of air in one second. In this case, the reference value is set at 0,000000000001 Watts per square meter.
Sound Pressure is a measure of FORCE per UNIT AREA
Sound Intensity is a measure of POWER per UNIT AREA
Let's see an example of how decibels work for sound intensity. This is how we compare a given value of intensity I to a reference value I0 using decibels. Due to the typically large variations, it is appropriate to use a logarithmic scale to the base 10 (understood in this equation). The multiplying factor 10 appears because we are using decibels and not bels, and the 'SIL' indicates that we are dealing with Sound Intensity Levels:
being 0,000000000001 our reference value and 0,0000001 our measured value we have:
which is equal to
which is our measured value compared to the reference level, so
0dB(SIL)= 0,000000000001 watts per square meter
50dB(SIL)= 0,0000001 watts per square meter
and look at this, this is very important:
let's say we measure a value of 0,0000002, twice as much intensity than 50dB(SIL)
the result in dB(SIL) will be equal to
so passing from 50dB(SIL) to 53dB(SIL) is equal to doubling the intensity level. This is valid for any given value, whatever high or low: a 3dB(SIL) increase means a double amount of sound intensity, so 3dB(SIL) is equal to two times the intensity of 0dB(SIL), and 23dB(SIL) is equal to two times 20dB(SIL). 36dB(SIL) is equal to four times 30dB(SIL). Is it getting clearer?
Now, the 'SIL' that follows the 'dB' is the key to calculate our values: it tells us what measurements we are dealing with and therefore what reference value we should employ, here are a few examples:
dB(SPL) (Sound Pressure Level):
dB(SIL) (Sound Intensity Level):
dBm (electrical power):
dBu (voltage amplitude, or RMS):
Now we are getting closer to the point...
Outdoors, and without relevant obstacles, an ideal punctiform sound source emits vibrations in a spherical pattern: this means that the sound propagates equally in every direction.
We have said already that the intensity of a sound is the amount of energy that passes through a square meter of air in one second. However, is the sound pressure rather than its physical intensity that our eardrums react to; and in addition to this, sound intensity is quite difficult to measure. It is easier to measure sound pressure, and then relate it to intensity if we need. The relationship between sound intensity and sound pressure is the following:
The Greek letter 'rho' is a constant called 'air impedance', and it is determined by numerous factors such as air temperature, humidity, and so on. We won't go into details of this constant, because what is of most interest to us is that, in the same external conditions ( = if 'rho' does not change), intensity is proportional to the square of the pressure. So, if the pressure doubles, the intensity quadruples and so on. We can then say that the following equations are equivalent:
Both scales are based on the hearing threshold, so in terms of dB, they are also equivalent, however they compare very different values.
Let's get back to sound pressure:
Because of the logarithms properties, the logarithm of the square of a number is equal to two times the logarithm of that number:
This makes a huge difference, because in this case it is an increment of 6dB, and not 3 that doubles a given value.
Let's see an example:
0dB(spl) = 20µPa = 0,00002 Pa
and suppose we measure a pressure of 0,0632 Pa (which is more than 3000 times the reference pressure!)
being
which is the average level of the noise of a busy office or a restaurant for example. A normal quiet conversation is typically around 60dB(SPL), let's calculate what pressure does it exercise on our eardrums:
first of all we divide both sides by 20
which means that
So
Thus, we can simplify both sides
Which is equal to
60dB(SPL) exercise a pressure of 0,02Pa on our eardrum.
One last thing: both sound pressure and intensity decrease sensibly with distance, but not in the same way. The variation of pressure in relation to the distance is expressed by this formula:
dB(SPL)1 and 2 are respectively the sound pressure measured in a specific point (that is at a distance equal to d1 from the sound source) and the sound pressure that would be measured at a distance equal to d2.
So imagine that we are measuring 60 dB(SPL) at 2 meter from the sound source. How much pressure would we measure if we move away so that the distance is 4 meters?
which is a 6dB(SPL) decrease (= 1/2 of the pressure in d1).
Let's take a look at what happens to sound intensity:
and
which is exactly one quarter of the initial value: doubling the distance means that the pressure will be 1/2 of the initial value (inversely proportional to the distance) and that the sound intensity will be 1/4 of the initial value (inversely proportional to the squared distance), which is also confirmed by the relation between intensity and pressure, being 'rho' constant.
Well, that was pretty intense wasn't it?
make sure you are extremely familiar with all the above before going on: make plenty of exercises and tests on this as it is going to be used really often.
--
[1] (Rowlett, 2004 [Online])
[2] (ibid.)
The amplitude of a sound wave is strictly connected to how loud that sound is perceived. In order to introduce a unit of measure for sound loudness, we need to understand how our ears perceive sound. More will be said about the anatomy of the ear, for now let's quickly focus on the eardrum: a very thin membrane that is able to detect even the slightest air vibration. When a vibrating object generates vibrations in the air, the vibrating air hits our eardrums, whose movements are then transduced into electric impulses that are transmitted to our brain which interprets them as sound.
Our perception of sound, is connected with the pressure exercised on our eardrums, but not in direct proportion. If the relation between air pressure and perceived loudness were linear (or direct), we could say that applying twice as much pressure on our eardrum would result in a twice as loud sound. Well, it is not quite so: the pressure exercised on our eardrums and the loudness that we feel are connected by a logarithmic proportion, not by a direct one. At very low pressure levels, we are able to distinguish slight variations very clearly. The higher the pressure, the more the pressure must be increased in order for us to perceive the same increment in loudness.
Confused? Look at the following graph:
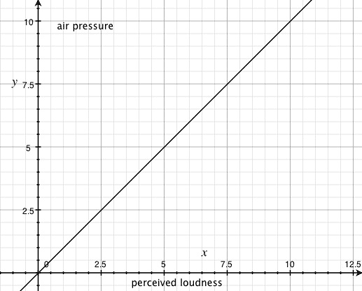
As you can see, in this graph the pressure (x) and the perceived loudness (y) are directly proportional, so when one increases, the other one increases of the same amount.
OUR EARS DON'T WORK LIKE THAT!!!!
This is more like it:
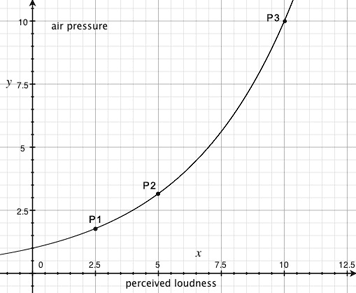
Let's not talk about units of measure for the moment (this graph is for demonstration only), but according to this graph, to a loudness of 2,5 corresponds a pressure of 1,7 (P1). In order to feel the sound twice as loud, we need the pressure to rise up to 3,14(P2): an increment of 1,44 units of pressure, which we will perceive with a loudness of 5. Now, if we would want to feel the sound with a loudness of 10, hence doubling the current loudness, the pressure exercised on our eardrums must be 10 units of pressure (P3), an increment of 6,86. Doubling this last value of loudness would make our eardrums bare a pressure value of about 100 units of pressure (not on graph): an increment of 90 units!
So, let's compare the two proportions in a chart:
LINEAR |
LOGARITHMIC |
||
Loudness |
Pressure |
Loudness |
Pressure |
2,5 |
2,5 |
2,5 |
1,7 |
5 |
5 |
5 |
3,14 |
10 |
10 |
10 |
10 |
20 |
20 |
20 |
100 |
This is the way our ears work, so the kind of values we have do deal with range from extremely low to extremely high, which is not exactly convenient when it comes to operations and calculations. If we could have a logarithmic scale to measure the pressure variations we could kind of 'rectify' the curve on the graph and have much practical values to deal with.
Rectified graph:
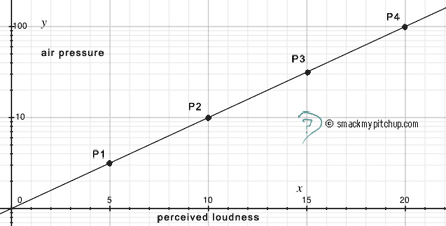
As you can see, by applying a logarithmic scale to the y axis, we are here dealing with much more convenient numbers and values, and we can also see pressure value P4, which was not visible using a linear scale.
This is why at Bell Telephone Laboratories telecommunication engineers have elaborated a unit of measure that suits the ear's behaviour. The Bel.
The Bel (in honour of Alexander Graham Bell) is a very particular measurement scale, mostly because is used to meter relative and not absolute values.
A Bel, or its submultiple decibel (dB), is not a unit of measurement itself, since it does not measure anything in particular: it expresses a logarithmic relationship between a given value and its reference value. Those values can be any kind of values: voltage, power, intensity, and, in our case, sound pressure or sound intensity. The reference value (the 0dB) is usually the minimum value employed for that measurement. In case of sound pressure, the minimum value is defined as the pressure exercised on the human eardrum by the softest sound audible. In other words, it is the softest sound a human can hear. By convention this sound pressure level is set at 20 micropascal (20 µPa).
A Pascal (Pa) is a unit of pressure:
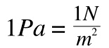
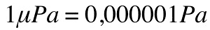
'N' stands for Newton, a unit of force, defined as such:
"A force of one Newton will accelerate a mass of one kilogram at the rate of one meter per second per second" [2]
Another way we can measure the power of a sound wave is measuring its intensity: sound intensity is a measure of sound power per unit area and it is measured in Watts per square meter.
1W = 1Joule/1s
"A joule is the amount of energy necessary to exert a force of 1 Newton for a distance of 1 meter" [3] so:
1W = 1N*1m/1s
Intensity is the amount of energy that passes through a square meter of air in one second. In this case, the reference value is set at 0,000000000001 Watts per square meter.
Sound Pressure is a measure of FORCE per UNIT AREA
Sound Intensity is a measure of POWER per UNIT AREA
Let's see an example of how decibels work for sound intensity. This is how we compare a given value of intensity I to a reference value I0 using decibels. Due to the typically large variations, it is appropriate to use a logarithmic scale to the base 10 (understood in this equation). The multiplying factor 10 appears because we are using decibels and not bels, and the 'SIL' indicates that we are dealing with Sound Intensity Levels:
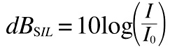
being 0,000000000001 our reference value and 0,0000001 our measured value we have:
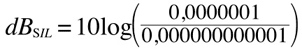
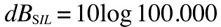
which is equal to
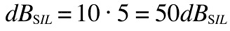
which is our measured value compared to the reference level, so
0dB(SIL)= 0,000000000001 watts per square meter
50dB(SIL)= 0,0000001 watts per square meter
and look at this, this is very important:
let's say we measure a value of 0,0000002, twice as much intensity than 50dB(SIL)
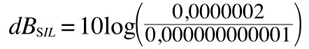
the result in dB(SIL) will be equal to
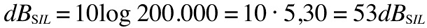
so passing from 50dB(SIL) to 53dB(SIL) is equal to doubling the intensity level. This is valid for any given value, whatever high or low: a 3dB(SIL) increase means a double amount of sound intensity, so 3dB(SIL) is equal to two times the intensity of 0dB(SIL), and 23dB(SIL) is equal to two times 20dB(SIL). 36dB(SIL) is equal to four times 30dB(SIL). Is it getting clearer?
Now, the 'SIL' that follows the 'dB' is the key to calculate our values: it tells us what measurements we are dealing with and therefore what reference value we should employ, here are a few examples:
dB(SPL) (Sound Pressure Level):
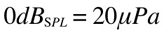
dB(SIL) (Sound Intensity Level):
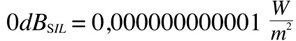
dBm (electrical power):
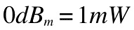
dBu (voltage amplitude, or RMS):
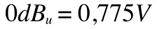
Now we are getting closer to the point...
Outdoors, and without relevant obstacles, an ideal punctiform sound source emits vibrations in a spherical pattern: this means that the sound propagates equally in every direction.
We have said already that the intensity of a sound is the amount of energy that passes through a square meter of air in one second. However, is the sound pressure rather than its physical intensity that our eardrums react to; and in addition to this, sound intensity is quite difficult to measure. It is easier to measure sound pressure, and then relate it to intensity if we need. The relationship between sound intensity and sound pressure is the following:
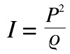
The Greek letter 'rho' is a constant called 'air impedance', and it is determined by numerous factors such as air temperature, humidity, and so on. We won't go into details of this constant, because what is of most interest to us is that, in the same external conditions ( = if 'rho' does not change), intensity is proportional to the square of the pressure. So, if the pressure doubles, the intensity quadruples and so on. We can then say that the following equations are equivalent:
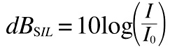
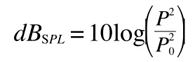
Both scales are based on the hearing threshold, so in terms of dB, they are also equivalent, however they compare very different values.
Let's get back to sound pressure:
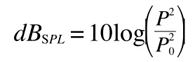
Because of the logarithms properties, the logarithm of the square of a number is equal to two times the logarithm of that number:
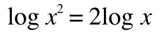
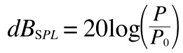
This makes a huge difference, because in this case it is an increment of 6dB, and not 3 that doubles a given value.
Let's see an example:
0dB(spl) = 20µPa = 0,00002 Pa
and suppose we measure a pressure of 0,0632 Pa (which is more than 3000 times the reference pressure!)
being
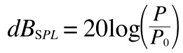
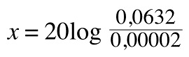
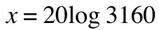
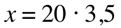
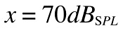
which is the average level of the noise of a busy office or a restaurant for example. A normal quiet conversation is typically around 60dB(SPL), let's calculate what pressure does it exercise on our eardrums:
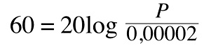
first of all we divide both sides by 20
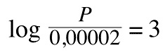
which means that
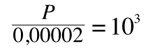
So
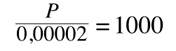
Thus, we can simplify both sides
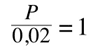
Which is equal to
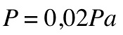
60dB(SPL) exercise a pressure of 0,02Pa on our eardrum.
One last thing: both sound pressure and intensity decrease sensibly with distance, but not in the same way. The variation of pressure in relation to the distance is expressed by this formula:
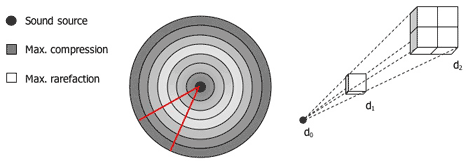
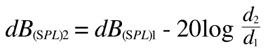
dB(SPL)1 and 2 are respectively the sound pressure measured in a specific point (that is at a distance equal to d1 from the sound source) and the sound pressure that would be measured at a distance equal to d2.
So imagine that we are measuring 60 dB(SPL) at 2 meter from the sound source. How much pressure would we measure if we move away so that the distance is 4 meters?
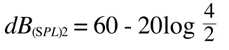
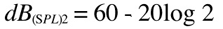
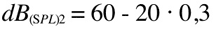
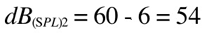
which is a 6dB(SPL) decrease (= 1/2 of the pressure in d1).
Let's take a look at what happens to sound intensity:
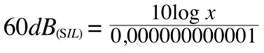
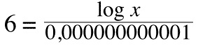
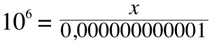
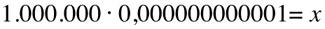
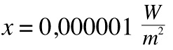
and
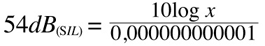
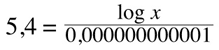
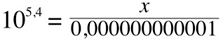
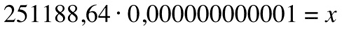
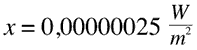
which is exactly one quarter of the initial value: doubling the distance means that the pressure will be 1/2 of the initial value (inversely proportional to the distance) and that the sound intensity will be 1/4 of the initial value (inversely proportional to the squared distance), which is also confirmed by the relation between intensity and pressure, being 'rho' constant.
Well, that was pretty intense wasn't it?
make sure you are extremely familiar with all the above before going on: make plenty of exercises and tests on this as it is going to be used really often.
--
[1] (Rowlett, 2004 [Online])
[2] (ibid.)
