notes
We all know that music is made of notes, but what is exactly a note?
"a single tone of definite pitch made by a musical instrument or the human voice" [1]
or
"a written sign representing the pitch and duration of such a sound". [1]
We can easily see that a note is strictly connected with the concept of pitch and duration of a sound. The term 'note' refers both to the sound and to the symbol that represents that sound. For this class, we will concentrate on the 'sound' part, while in the next class we will see how these sounds are represented.
The notation system we will be dealing with in this course is the Western Music system, or diatonic, which is made of seven notes and their alterations, for a total of 12 equal intervals per octave. It is good to know, though, that this is not the only notation system. Other countries, especially in the Indian and Asian regions, use different systems, and experimentations of different subdivision methods has been carried out in Europe as well, with the most famous experimental musical movements rising in the early 1900.
The system currently in use in western countries was initiated by the Italian Guido d'Arezzo, a monk who lived from 995 to 1050 AC.
Basically, this system uses seven notes, that are represented by Latin letters:
In some countries, they are actually called
But there is absolutely no difference in pitch.
The seven notes are progressively raising in pitch, the 8th note would be another C, exactly an octave higher than the first one (octave actually means 'the eighth' in Latin). Let's have a look at them on a piano keyboard, which you should be more familiar with:
This is one octave on a piano keyboard, which represents very well the way notes are related to each other: each of the white keys, is a note, we can see that there are seven of them in an octave, the first note being a C.
How are they related to pitch? Well, we have already said that two sounds have an interval of an octave between them when one is twice the frequency of the other, so if our 'C' is a 261Hz note, the immediately higher 'C' will be 522Hz, while the one immediately below 130,5Hz.
The 'distance', or better 'interval', between two white keys is one tone, which is equal to two semitones, with the exception of the E-F and B-C intervals which are only one semitone. This is clearly visible from the presence of black keys between white keys. So what are the black keys? Aren't they notes either? Well, black keys represent what are commonly known as 'altered notes': altered notes present a 'b' (pronounced 'flat') or a '#' (pronounced 'sharp') sign next to them to indicate that the sound is slightly flattened or sharpened respectively.
So, in the current western system there is a one tone interval between two given notes A and B. We can say that an A# is a note whose pitch is exactly halfway through an A and a B. A Bb is a note whose pitch is almost halfway through an A and a B.
Yes, that is correct, they are exactly the same note! Now, let's say that an octave is divided into 12 semitones:
- A semitone is the smallest pitch variation in western music
- Semitones are equally distributed across an octave, which means that the pitch variation between an A and an A# is the same as between a C and a C#
- This subdivision is called 'equally tempered system'.
These two ways of writing the 12 intervals in an octave are exactly equivalent. Depending on musical formal conventions, it could be more appropriate to use the sharp or the flat notation, but in terms of pitch nothing changes.
Notes and their frequency are related by a mathematical proportion: the frequency that we use to calculate other notes' frequencies is the one of the 'central A' (or A4), which is conventionally set at 440Hz. The name comes from the fact that it is the A of the fourth octave of a piano keyboard, and the central note. Once we are familiar with the concept of semitones, we can easily calculate the frequency of any note with the following formula:
where 'n' is the number of semitones that separate the note from A4. Let's try it and see what is the frequency of the E immediately below A4, which will be an E4: first of all we need to know the distance in semitones
So there are 5 semitones between A4 and E4, and since we are decreasing the pitch, that would be a -5.
We also finally have the relation between octaves and frequencies explained mathematically: there are 12 semitones in an octave, therefore the formula would be:
In modern instruments, especially in MIDI virtual instruments, we also find a finer intervals scale called 'cents'. This scale's smallest unit is 1/100 of a semitone, and allow the musician to set a very fine tuning. It follows that according to this scale, semitones are all 100 cents apart, and there are 1200 cents in an octave. The minimum noticeable variation in pitch by the human ear is conventionally set at 5 cents.
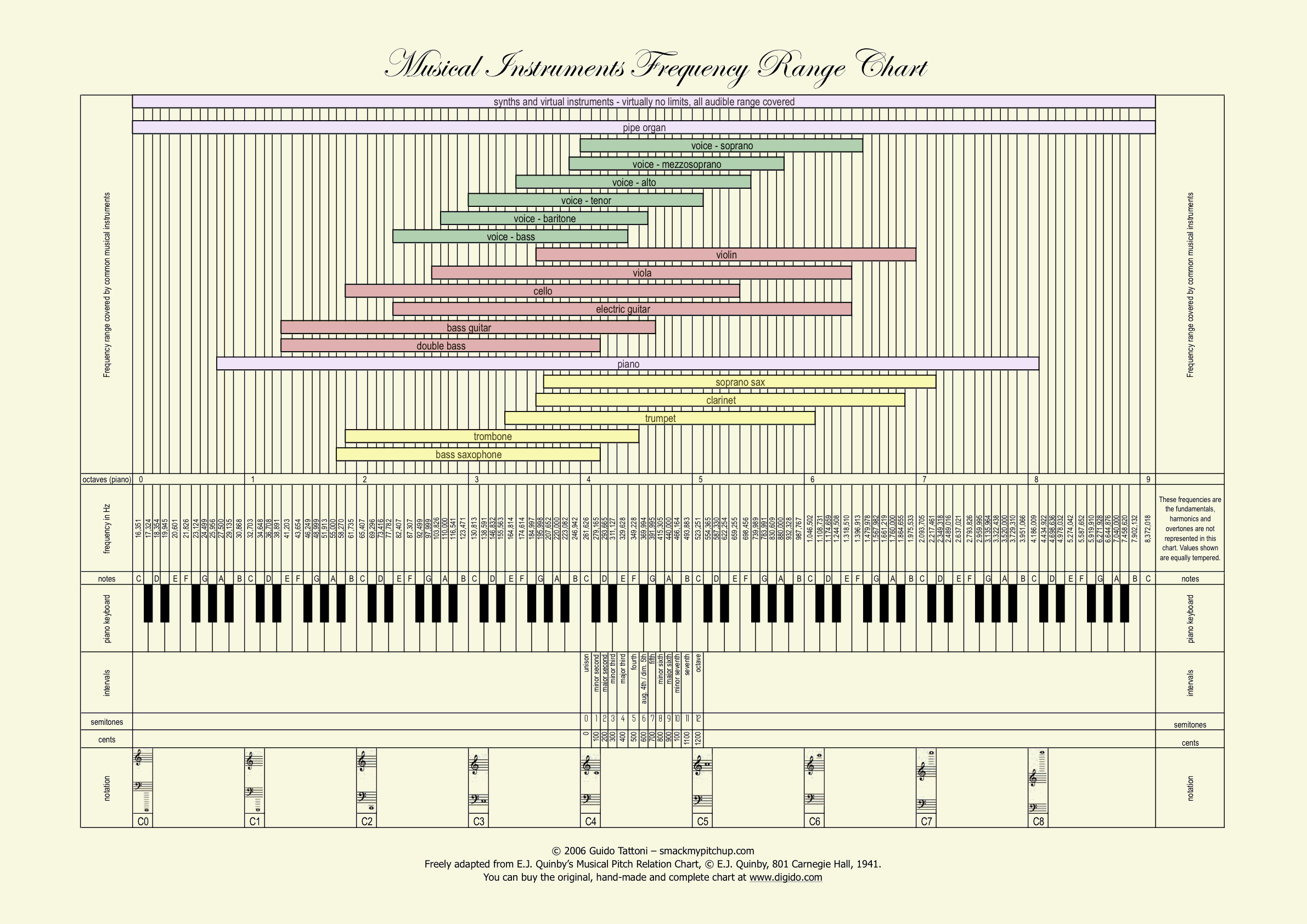
We have already seen that across the audible frequency range, we can identify ten octaves: of course, not every instrument is able to reproduce such a wide range of notes. Most musical instruments can reproduce 3 to 6 octaves, and the human voice is no exception. Please note that when we talk about frequency related to notes, we mean the frequency of the fundamental note only, and not harmonics and overtones. The range of notes an instrument can reproduce is called extension, while the overall frequencies that are produced by playing it, including harmonics and overtones, is called frequency range.
The pipe organ and the piano are the traditional instruments that have the widest extension (9 and 7 octaves respectively), and the harp follows closely with 6 octaves. Other instruments, as we said, are more limited. The limited possibilities of each instruments are related to their physical dimensions (strings or pipes length, etc.). As opposed to the traditional orchestra instruments, nowadays there is a vast amount of electronic and digital instruments, whose extension has virtually no limits, since they are free from the limitations of a real instrument.
This chart
summarises the extension of the most common instruments in relation to notes and frequencies.
Ignore the musical notation for now, which will be the subject of the next class.
----------
[1] (New Oxford American Dictionary, 2005)
"a single tone of definite pitch made by a musical instrument or the human voice" [1]
or
"a written sign representing the pitch and duration of such a sound". [1]
We can easily see that a note is strictly connected with the concept of pitch and duration of a sound. The term 'note' refers both to the sound and to the symbol that represents that sound. For this class, we will concentrate on the 'sound' part, while in the next class we will see how these sounds are represented.
The notation system we will be dealing with in this course is the Western Music system, or diatonic, which is made of seven notes and their alterations, for a total of 12 equal intervals per octave. It is good to know, though, that this is not the only notation system. Other countries, especially in the Indian and Asian regions, use different systems, and experimentations of different subdivision methods has been carried out in Europe as well, with the most famous experimental musical movements rising in the early 1900.
The system currently in use in western countries was initiated by the Italian Guido d'Arezzo, a monk who lived from 995 to 1050 AC.
Basically, this system uses seven notes, that are represented by Latin letters:
In some countries, they are actually called
But there is absolutely no difference in pitch.
The seven notes are progressively raising in pitch, the 8th note would be another C, exactly an octave higher than the first one (octave actually means 'the eighth' in Latin). Let's have a look at them on a piano keyboard, which you should be more familiar with:
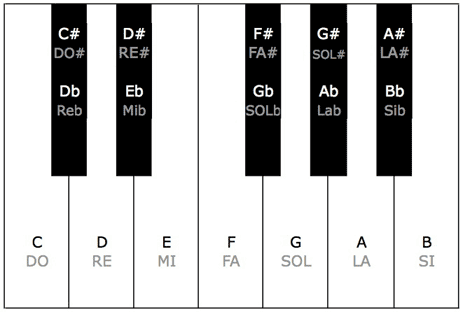
This is one octave on a piano keyboard, which represents very well the way notes are related to each other: each of the white keys, is a note, we can see that there are seven of them in an octave, the first note being a C.
How are they related to pitch? Well, we have already said that two sounds have an interval of an octave between them when one is twice the frequency of the other, so if our 'C' is a 261Hz note, the immediately higher 'C' will be 522Hz, while the one immediately below 130,5Hz.
The 'distance', or better 'interval', between two white keys is one tone, which is equal to two semitones, with the exception of the E-F and B-C intervals which are only one semitone. This is clearly visible from the presence of black keys between white keys. So what are the black keys? Aren't they notes either? Well, black keys represent what are commonly known as 'altered notes': altered notes present a 'b' (pronounced 'flat') or a '#' (pronounced 'sharp') sign next to them to indicate that the sound is slightly flattened or sharpened respectively.
So, in the current western system there is a one tone interval between two given notes A and B. We can say that an A# is a note whose pitch is exactly halfway through an A and a B. A Bb is a note whose pitch is almost halfway through an A and a B.
Yes, that is correct, they are exactly the same note! Now, let's say that an octave is divided into 12 semitones:
- A semitone is the smallest pitch variation in western music
- Semitones are equally distributed across an octave, which means that the pitch variation between an A and an A# is the same as between a C and a C#
- This subdivision is called 'equally tempered system'.
| # | C | C# | D | D# | E | F | F# | G | G# | A | A# | B | C |
| b | C | Db | D | Eb | E | F | Gb | G | Ab | A | Bb | B | C |
| semitones | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
These two ways of writing the 12 intervals in an octave are exactly equivalent. Depending on musical formal conventions, it could be more appropriate to use the sharp or the flat notation, but in terms of pitch nothing changes.
Notes and their frequency are related by a mathematical proportion: the frequency that we use to calculate other notes' frequencies is the one of the 'central A' (or A4), which is conventionally set at 440Hz. The name comes from the fact that it is the A of the fourth octave of a piano keyboard, and the central note. Once we are familiar with the concept of semitones, we can easily calculate the frequency of any note with the following formula:
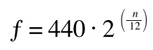
where 'n' is the number of semitones that separate the note from A4. Let's try it and see what is the frequency of the E immediately below A4, which will be an E4: first of all we need to know the distance in semitones
| Note | A | G# | G | F# | F | E |
| Distance in semitones | 0 | -1 | -2 | -3 | -4 | -5 |
So there are 5 semitones between A4 and E4, and since we are decreasing the pitch, that would be a -5.
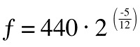
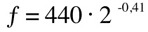
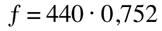
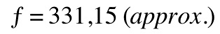
We also finally have the relation between octaves and frequencies explained mathematically: there are 12 semitones in an octave, therefore the formula would be:
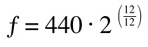
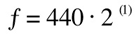
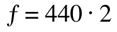
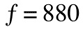
In modern instruments, especially in MIDI virtual instruments, we also find a finer intervals scale called 'cents'. This scale's smallest unit is 1/100 of a semitone, and allow the musician to set a very fine tuning. It follows that according to this scale, semitones are all 100 cents apart, and there are 1200 cents in an octave. The minimum noticeable variation in pitch by the human ear is conventionally set at 5 cents.
We have already seen that across the audible frequency range, we can identify ten octaves: of course, not every instrument is able to reproduce such a wide range of notes. Most musical instruments can reproduce 3 to 6 octaves, and the human voice is no exception. Please note that when we talk about frequency related to notes, we mean the frequency of the fundamental note only, and not harmonics and overtones. The range of notes an instrument can reproduce is called extension, while the overall frequencies that are produced by playing it, including harmonics and overtones, is called frequency range.
The pipe organ and the piano are the traditional instruments that have the widest extension (9 and 7 octaves respectively), and the harp follows closely with 6 octaves. Other instruments, as we said, are more limited. The limited possibilities of each instruments are related to their physical dimensions (strings or pipes length, etc.). As opposed to the traditional orchestra instruments, nowadays there is a vast amount of electronic and digital instruments, whose extension has virtually no limits, since they are free from the limitations of a real instrument.
This chart
summarises the extension of the most common instruments in relation to notes and frequencies.
Ignore the musical notation for now, which will be the subject of the next class.
----------
[1] (New Oxford American Dictionary, 2005)