Logarithms
Before continuing, it is important that we make sure we have an understanding of what a logarithm is: the reason is that many measurements and values in sound engineering are expressed in a logarithmic scale, we will deal with the first of them in the next lesson.
A logarithm is defined as:
"a quantity representing the power to which a fixed number (the base) must be raised to produce a given number" [1]
In other words we can say that logarithm are the inverse operation of a root extraction.
In the function
x is the number that raised to the third is equal to 8, which is 2. By extracting roots, we find a base (x) to a given exponent (3), in order for it to be equal to a given value (8). So we answer to the question 'what is the number that raised to the third is equal to 8?'
But what if we want to find to what power (x) should a given number (a) be raised in order for it to be equal to another given number (b)?
this is when logarithms come into place:
if:
then:
'2' is called the base of the logarithm
The most common base in sound engineering is 10.
For example:
if you see a logarithmic function with no base indicated, that means that the base is 10:
when writing a function of a log base 10 of a given number, the 10 is understood, so
A few things to remember:
Laws of Logarithms:
1. log product is equal to the sum of logs.
Example:
2. log of a quotient is equal to the difference between logs.
Example:
3. log number to a power equals power times log of a number. (we are going to use this soon!)
base change:
where a and b are any valid base
--
[1] New Oxford American Dictionary, 2005
A logarithm is defined as:
"a quantity representing the power to which a fixed number (the base) must be raised to produce a given number" [1]
In other words we can say that logarithm are the inverse operation of a root extraction.
In the function
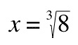
x is the number that raised to the third is equal to 8, which is 2. By extracting roots, we find a base (x) to a given exponent (3), in order for it to be equal to a given value (8). So we answer to the question 'what is the number that raised to the third is equal to 8?'
But what if we want to find to what power (x) should a given number (a) be raised in order for it to be equal to another given number (b)?
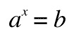
this is when logarithms come into place:
if:
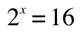
then:
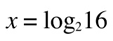
'2' is called the base of the logarithm
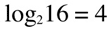
The most common base in sound engineering is 10.
For example:
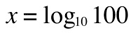
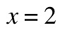
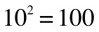
if you see a logarithmic function with no base indicated, that means that the base is 10:
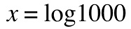
when writing a function of a log base 10 of a given number, the 10 is understood, so
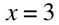
A few things to remember:
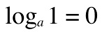 because
because 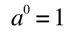
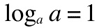 because
because 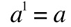
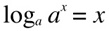 because
because 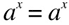
if 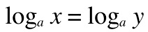 then
then 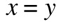
Laws of Logarithms:
1. log product is equal to the sum of logs.
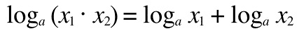
Example:
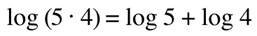
2. log of a quotient is equal to the difference between logs.
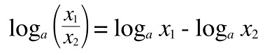
Example:
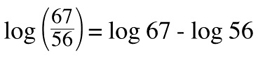
3. log number to a power equals power times log of a number. (we are going to use this soon!)
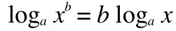
base change:
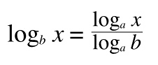
where a and b are any valid base
--
[1] New Oxford American Dictionary, 2005
