shapes
Before analysing some 'real instruments' waveforms, it is worth having a look at the most common complex periodical waveforms: these waveforms, whilst retaining the periodical qualities of pure tones, are made by summing a fundamental frequency with its harmonics in different proportions.
1. square waves
This waveform is called a square wave, and it contains a fundamental frequency and odd series of harmonics of decreasing amplitudes. By odd series we only mean odd numbered harmonics only (3rd, 5th, 7th, etc). The amplitude of the harmonics is equal to 1 divided by the respective harmonic number, so that the third harmonic's amplitude is 1/3 of he fundamental, the fifth's is 1/5 and so on. You can clearly see this proportion in the FFT.
2. triangle waves
A triangle wave's harmonic distribution is the same as the square wave (fundamental + odd harmonics), but the amplitude relationship is different: The amplitude of the harmonics is equal to 1 divided by the squared respective harmonic number, so that the third harmonic's amplitude is 1/9 of he fundamental, the fifth's is 1/25 and so on.
3. sawtooth waves
A sawtooth wave contains a complete series of harmonics (odd and even), related as they are in a square wave: the amplitude of the harmonics is equal to 1 divided by the respective harmonic number, so that the second harmonic's amplitude is 1/2 of he fundamental, the third's is 1/3 and so on.
The sounds represented by such precise sound waves are in fact 'ideal', the actual shape of these sound waves would be slightly different: remember that a vertical line in an amplitude (y) and time (x) graph means time=0!
These waveforms are very rare to find in nature: they are commonly generated by oscillators, and they are often used in synthesis to generate even more complex sounds.
Real instruments sounds are much more complex than these waveforms: first of all they are usually not periodic, so they do not repeat themselves in regular cycles, and they contain harmonics whose amplitude is not specifically related by mathematical proportions. They also contain the overtones that we have discussed earlier. The following three sounds have the same fundamental frequency, but an FFT taken at 1.00 second reveals a very different frequency content:
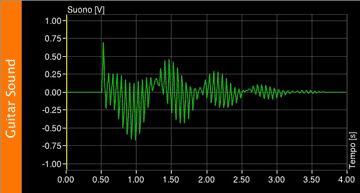
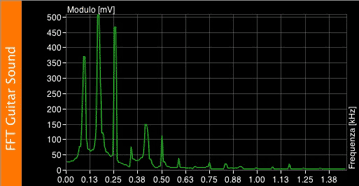
This is a guitar string plucked and its FFT
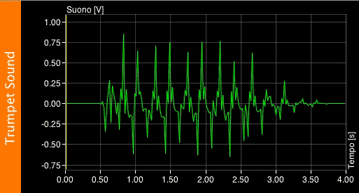
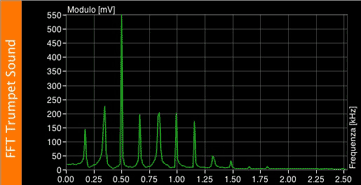
This is a trumpet's note
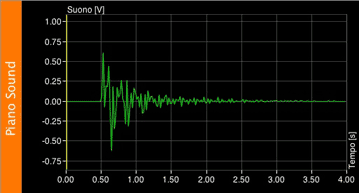
And this is a piano note
This leads us to differentiate between noise and sound: now we have the knowledge necessary to be able to understand which one is which. As we have seen, musical instruments sounds contain frequencies that are related by a mathematical proportion, and therefore sound to us as harmonious or meaningful. We perceive as noise the sounds that do not present such relations, and consist of frequencies that are not related by a specific proportion or periodicity.
This of course is just a technical definition, but things in reality may be very different: some times we define as 'noise' the music coming from our neighbour's apartment when we are trying to sleep, or, on the other hand, we hear 'extraneous' sounds that we would consider noises in a musical composition, sitting surprisingly well with more 'musical' sounds. As you can see many things are very subjective when is comes to our hearing!
Frequency content however, is not the only quality that determines the timbre of a sound. In the next lesson we will take a look at the envelope.
1. square waves
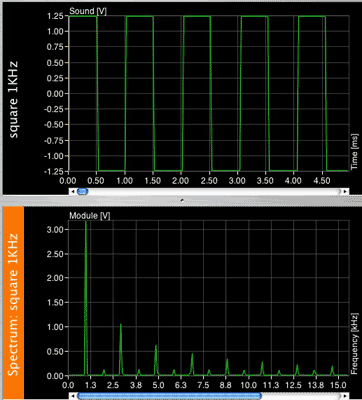
This waveform is called a square wave, and it contains a fundamental frequency and odd series of harmonics of decreasing amplitudes. By odd series we only mean odd numbered harmonics only (3rd, 5th, 7th, etc). The amplitude of the harmonics is equal to 1 divided by the respective harmonic number, so that the third harmonic's amplitude is 1/3 of he fundamental, the fifth's is 1/5 and so on. You can clearly see this proportion in the FFT.
2. triangle waves
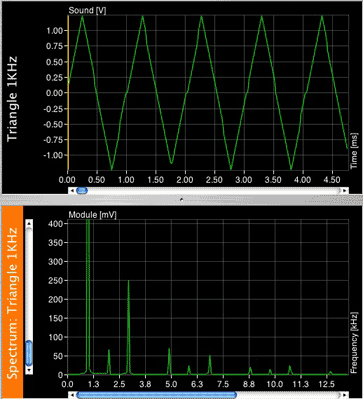
A triangle wave's harmonic distribution is the same as the square wave (fundamental + odd harmonics), but the amplitude relationship is different: The amplitude of the harmonics is equal to 1 divided by the squared respective harmonic number, so that the third harmonic's amplitude is 1/9 of he fundamental, the fifth's is 1/25 and so on.
3. sawtooth waves
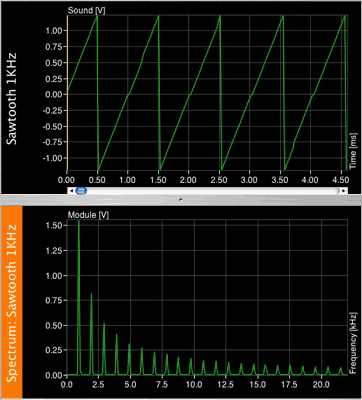
A sawtooth wave contains a complete series of harmonics (odd and even), related as they are in a square wave: the amplitude of the harmonics is equal to 1 divided by the respective harmonic number, so that the second harmonic's amplitude is 1/2 of he fundamental, the third's is 1/3 and so on.
The sounds represented by such precise sound waves are in fact 'ideal', the actual shape of these sound waves would be slightly different: remember that a vertical line in an amplitude (y) and time (x) graph means time=0!
These waveforms are very rare to find in nature: they are commonly generated by oscillators, and they are often used in synthesis to generate even more complex sounds.
Real instruments sounds are much more complex than these waveforms: first of all they are usually not periodic, so they do not repeat themselves in regular cycles, and they contain harmonics whose amplitude is not specifically related by mathematical proportions. They also contain the overtones that we have discussed earlier. The following three sounds have the same fundamental frequency, but an FFT taken at 1.00 second reveals a very different frequency content:
This is a guitar string plucked and its FFT
This is a trumpet's note
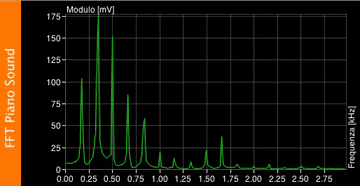
And this is a piano note
This leads us to differentiate between noise and sound: now we have the knowledge necessary to be able to understand which one is which. As we have seen, musical instruments sounds contain frequencies that are related by a mathematical proportion, and therefore sound to us as harmonious or meaningful. We perceive as noise the sounds that do not present such relations, and consist of frequencies that are not related by a specific proportion or periodicity.
This of course is just a technical definition, but things in reality may be very different: some times we define as 'noise' the music coming from our neighbour's apartment when we are trying to sleep, or, on the other hand, we hear 'extraneous' sounds that we would consider noises in a musical composition, sitting surprisingly well with more 'musical' sounds. As you can see many things are very subjective when is comes to our hearing!
Frequency content however, is not the only quality that determines the timbre of a sound. In the next lesson we will take a look at the envelope.
