peak vs rms
There is more we should say about how human ears react to pressure changes: so far we have related pressure changes to loudness without taking into account a very important factor: time.
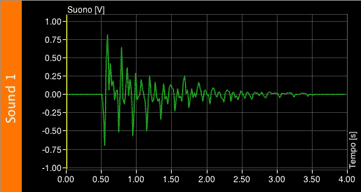
Let's take for example this sound wave: it has a few high peaks, but most of them are at a lower level:
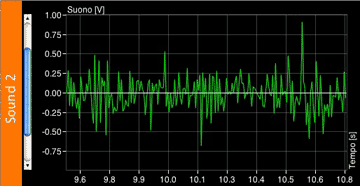
And another wave could have consistently high amplitude peaks, like this:
Considering that the highest peaks of both waves are at the same amplitude, will they be perceived as equally loud?
No, because loudness is not perceived from transients (so are called brief peaks of high amplitude that are very short in time), but from the average of the pressure exercised on our eardrums. However, since our waveform is made of positive and negative peaks, its average mathematical amplitude would be very close to zero, which is not what happens in reality, since negative peaks also represent a variation of pressure. This is why we calculate the average pressure using a 'root mean square' (RMS), which is the square root of the average of the squares of the amplitude values. By squaring the negative values, we will make them positive, so that they would contribute to the average as they do in nature. Mathematically what we do is:
Having N values of amplitude
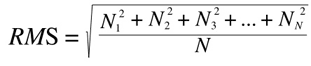
So in case of a sine whose peaks are at amplitude 1, the RMS value of the sound pressure level would be:
Using 5 values equally distributed across the whole dynamic range:
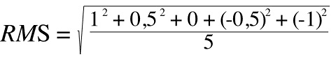

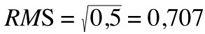
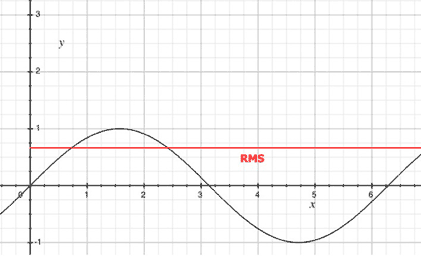
So let's compare the peak and the RMS curves:
While mixing we must keep an eye on both peaks and RMS levels, and we can do that thanks to PPM Meters (Peak Program Meter) and VU (Volume Units) meters respectively.
Let's take for example this sound wave: it has a few high peaks, but most of them are at a lower level:

And another wave could have consistently high amplitude peaks, like this:

Considering that the highest peaks of both waves are at the same amplitude, will they be perceived as equally loud?
No, because loudness is not perceived from transients (so are called brief peaks of high amplitude that are very short in time), but from the average of the pressure exercised on our eardrums. However, since our waveform is made of positive and negative peaks, its average mathematical amplitude would be very close to zero, which is not what happens in reality, since negative peaks also represent a variation of pressure. This is why we calculate the average pressure using a 'root mean square' (RMS), which is the square root of the average of the squares of the amplitude values. By squaring the negative values, we will make them positive, so that they would contribute to the average as they do in nature. Mathematically what we do is:
Having N values of amplitude
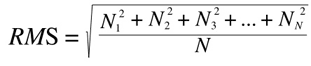
So in case of a sine whose peaks are at amplitude 1, the RMS value of the sound pressure level would be:
Using 5 values equally distributed across the whole dynamic range:
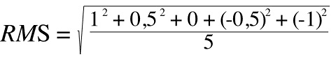

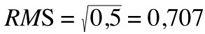
So let's compare the peak and the RMS curves:

While mixing we must keep an eye on both peaks and RMS levels, and we can do that thanks to PPM Meters (Peak Program Meter) and VU (Volume Units) meters respectively.
