phase
We have said already in lesson 3 that 'phase' is something we talk about only when more than one sound is involved. Phase (often represented by a Greek 'phi' or by a 'ø') expresses how two or more sounds are related in terms of time. It is particularly important, because as we will see phase difference is something that our brain uses in order to determine a sound's localisation. In other words, it is partly thanks to phase differences that we are able to know where a sound comes from. We said partly, because it is not the only data that our brain interprets in order to localise a sound.
First, let's take a look at the figure below: it is a circle of radius = 1.
Now, imagine a point (H) travelling around the circumference from point A to point B. The projection (HK) of this point on the segment AB will change according to the point's position on the circumference: the more H is distant, the longer will be HK. The segment OH forms an angle alpha with the segment OA. The length of the projection segment of point H on the AB axis is called 'sinalpha?. It follows that the length of the projection will vary according to the variation of alpha as:
When alpha = 0° then sinalpha = 0
When alpha = 90° then sinalpha = 1
When alpha = 180° then sinalpha = 0
When alpha = 270° then sinalpha = -1
When alpha = 360° then sinalpha = 0
Being the values above AB positive and the ones below negative. The variation of the values of sinalpha can be easily visualised in a graph representing the function
And guess what? It's a sine!
That's why we can refer to specific points of the sound wave with degree values: its peaks will be at 90° and 270°, while its zero-crossing at 0° and 180°.
This knowledge is necessary to understand the concept of phase.
Now, let's take a look at a 1Khz waveform:
As we know, compression and rarefaction alternate through time. Let's assume we are listening to this sound from a distance of 1,70m, knowing the speed of sound in air, we will easily calculate how long does it take to that sound to reach us and therefore hit our eardrums:
We know that time is equal to space divided by speed, so:
Since we know the 1Khz equals to 1000 cycles per second, the waveform will hit our eardrum after having done almost exactly five cycles. This is also confirmed by the fact that a wavelength of 34cm fits exactly five times in 1,70m.
Now, we add another sound source, which is also generating a 1KHz tone, but that is 8cm more distant: we are now listening to two identical sounds, one of which is at 1,70m and the other at 1,78. If the two sources start generating sound at the very same time, the sound that has to travel a longer distance will arrive to us a little later:
Which makes it a 0,23 milliseconds arrival time difference. It may seem not a major difference, but in fact it is. The second tone being delayed by 0,23ms is not in phase with the first one. Let's see what happens if we apply a 0,23ms delay to a second identical sine
Basically, when they reach our eardrum, the waveforms will be at different points of their cycles: precisely, the first one will be at 0° (A) and the second one will be at circa 270° (B). An almost 90° phase shift.
Two sound waves perfectly in phase have a 0° phase shift.
Two sound waves perfectly out of phase have a 180° (or 180° multiples) phase shift.
Phase shifts of 360° and multiples are equal to 0° shifts
Combining two identical sound waves will have different results according to their phase relation: in general, we can say that two waveforms whose amplitude is of the same sign (both positive, for example) will interact constructively (the sum of the amplitudes will be greater than the amplitudes of the single sound waves), if the signs are different they will interact destructively (the sum of the amplitudes will be lower than the amplitudes of the single sound waves). The two extreme events would be:
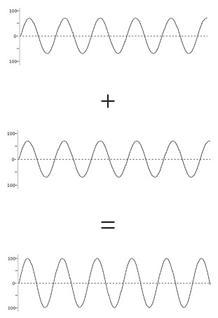
Two waves that are perfectly in phase will interact constructively, meaning the resulting sound wave's amplitude will be the sum of the original waves
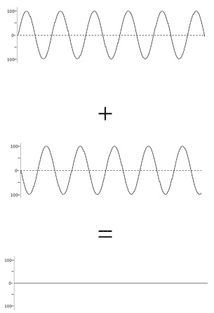
Two waves that are perfectly out phase will interact destructively, meaning the resulting sound wave's amplitude will be the difference of the original waves
Knowing the speed and the arrival time of two sounds of the same frequency, we can easily calculate their phase shift using the formula:
Let's try it with the two sound waves we have just used:
for a perfect 90° phase shift the arrival time difference must be
Which is exactly a quarter of 1ms, the period of 1KHz.
As we said, phase differences may affect sounds heavily, but we are going to talk about this when discussing the human perception of sound.
For now, make sure you do plenty of exercises, especially if you plan to take proficiency tests. In the test section, you will find plenty of tests to get familiar with all the calculations that we have dealt with so far.
First, let's take a look at the figure below: it is a circle of radius = 1.
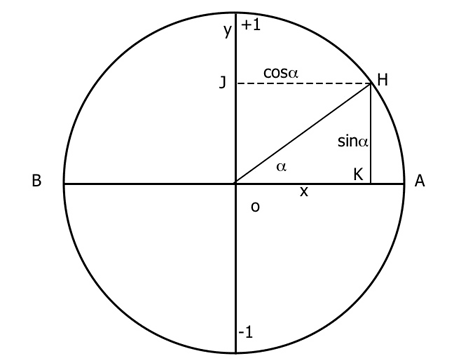
Now, imagine a point (H) travelling around the circumference from point A to point B. The projection (HK) of this point on the segment AB will change according to the point's position on the circumference: the more H is distant, the longer will be HK. The segment OH forms an angle alpha with the segment OA. The length of the projection segment of point H on the AB axis is called 'sinalpha?. It follows that the length of the projection will vary according to the variation of alpha as:
When alpha = 0° then sinalpha = 0
When alpha = 90° then sinalpha = 1
When alpha = 180° then sinalpha = 0
When alpha = 270° then sinalpha = -1
When alpha = 360° then sinalpha = 0
Being the values above AB positive and the ones below negative. The variation of the values of sinalpha can be easily visualised in a graph representing the function
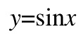
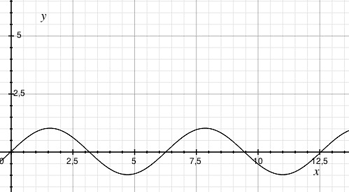
And guess what? It's a sine!
That's why we can refer to specific points of the sound wave with degree values: its peaks will be at 90° and 270°, while its zero-crossing at 0° and 180°.
This knowledge is necessary to understand the concept of phase.
Now, let's take a look at a 1Khz waveform:
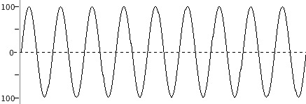
As we know, compression and rarefaction alternate through time. Let's assume we are listening to this sound from a distance of 1,70m, knowing the speed of sound in air, we will easily calculate how long does it take to that sound to reach us and therefore hit our eardrums:
We know that time is equal to space divided by speed, so:
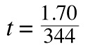
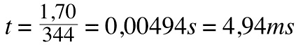
Since we know the 1Khz equals to 1000 cycles per second, the waveform will hit our eardrum after having done almost exactly five cycles. This is also confirmed by the fact that a wavelength of 34cm fits exactly five times in 1,70m.
Now, we add another sound source, which is also generating a 1KHz tone, but that is 8cm more distant: we are now listening to two identical sounds, one of which is at 1,70m and the other at 1,78. If the two sources start generating sound at the very same time, the sound that has to travel a longer distance will arrive to us a little later:
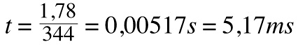
Which makes it a 0,23 milliseconds arrival time difference. It may seem not a major difference, but in fact it is. The second tone being delayed by 0,23ms is not in phase with the first one. Let's see what happens if we apply a 0,23ms delay to a second identical sine
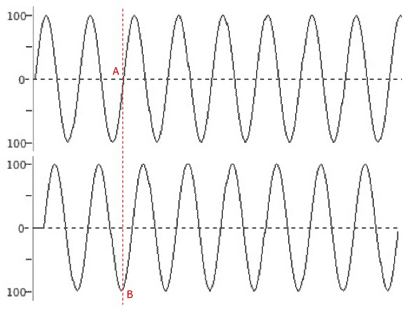
Basically, when they reach our eardrum, the waveforms will be at different points of their cycles: precisely, the first one will be at 0° (A) and the second one will be at circa 270° (B). An almost 90° phase shift.
Two sound waves perfectly in phase have a 0° phase shift.
Two sound waves perfectly out of phase have a 180° (or 180° multiples) phase shift.
Phase shifts of 360° and multiples are equal to 0° shifts
Combining two identical sound waves will have different results according to their phase relation: in general, we can say that two waveforms whose amplitude is of the same sign (both positive, for example) will interact constructively (the sum of the amplitudes will be greater than the amplitudes of the single sound waves), if the signs are different they will interact destructively (the sum of the amplitudes will be lower than the amplitudes of the single sound waves). The two extreme events would be:
Two waves that are perfectly in phase will interact constructively, meaning the resulting sound wave's amplitude will be the sum of the original waves
Two waves that are perfectly out phase will interact destructively, meaning the resulting sound wave's amplitude will be the difference of the original waves
Knowing the speed and the arrival time of two sounds of the same frequency, we can easily calculate their phase shift using the formula:
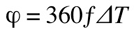
Let's try it with the two sound waves we have just used:
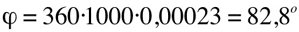
for a perfect 90° phase shift the arrival time difference must be
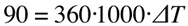
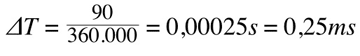
Which is exactly a quarter of 1ms, the period of 1KHz.
As we said, phase differences may affect sounds heavily, but we are going to talk about this when discussing the human perception of sound.
For now, make sure you do plenty of exercises, especially if you plan to take proficiency tests. In the test section, you will find plenty of tests to get familiar with all the calculations that we have dealt with so far.
